You do not need to do anything in this topic. But, please read it as it should help with your general understanding of how to develop models in MechDesigner.
Design of Kinematic-Chains
When you design a kinematic-chain (a mechanism) for a machine, it is important that you can control the position and motion of all of its Parts at all times! This is obvious and critically important.
MechDesigner applies two equations for you, all of the time and automatically.
For each kinematic-chain the equations analyze the:
•Degrees-of-Freedom
•Mobility
It is critical that the Mobility of a Kinematic-Chain is zero before you analyze the motion of a Part.
When the Mobility is zero, we say the kinematic-chain is kinematically-defined, or solved.
Degrees-of-Freedom (DOF):
The degrees-of-freedom of a kinematic-chain is the number of unique coordinates (angle or position) that you need to control to predict the position and motion of all Parts in the kinematic-chain
Parts: a Part you add (to the Mechanism-Plane) has 3 degrees-of-freedom. Joints: a Joint (Pin-Joint or Slide-Joint) removes 2 degrees-of-freedom. To calculate the DOF of a kinematic-chain that has Parts and Joints on a Plane, you can use this form of the Gruebler's equation.
Note: You do not need to know if the Joint is a Pin-Joint or a Slide-Joint. |
Mobility:
In MechDesigner, you control the position and motion of a coordinate with a Motion-Dimension FB.
When the number of Motion-Dimension FBs is equal to the number of Degrees-of-Freedom, we say the Mobility is zero, and the kinematic-chain is kinematically-defined. OR, we say the kinematic-chain solved. To calculate the Mobility of a kinematic-chain that has Parts and Joints on a Plane, you can use this form of the Kutzbach equation.
As an alternative, you can say that a Motion-Dimension FB removes one Degree-of-Freedom. Then, you can also say that the Mobility is zero when the number of Degrees-of-Freedom is equal to the number of Motion-Dimensions.
Note: You do not need to know if the Motion-Dimension FB controls the position and motion of a Rocker or a Slider. |
Degrees-of-Freedom and Mobility - Motion-Parts and Dyads.
Motion-Parts :
Example: Rocker dyad. The Motion-Part we use as an example is not important, as the equations do not need the type of joints or which coordinate the Motion-Dimension FB controls. |
||
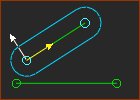 + 1 Part = 3 DoF |
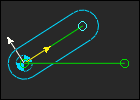 + 1 Joint = –2 DoF |
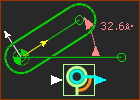 M=DoF–Mot-Dim FBs |
A Motion-Part does not change the number of degrees-of-freedom (DOF) of a kinematic-chain. Why? A Motion-Part is one Part, one Joint, and one Motion-Dimension + One Part: 1 × +3×DOF = +3×DOF + One Joint: +1 × –2×DOF = –2×DOF Thus, total DOF = +3 + (–2) = 1 Or, use the Gruebler's Equation
+ One Motion-Dimension FB controls 1 coordinate. Thus: Mobility = # DOF – # Motion-Dimension FBs = 1 – 1 = 0 (Perfect) Or use the Kutzbach Equation:
Thus the Motion-Part is kinematically-defined and solved. |
||
Dyads :
Example: R-R-R dyad. The dyad we use as an example is not important, as the equations does not need the type of joints. If you join the two Parts in a dyad to one 'other' Part, you design a structure. It is exactly equivalent to adding the Parts to two other Parts, when the two 'other' Parts are kinematically-defined. |
||
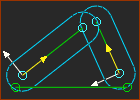 +2 Parts = 6 DoF |
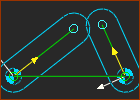 2 Joints = –2 –2 DoF |
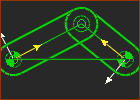 +1 Joint = –2 DoF |
A dyad does not change the number of degrees-of-freedom (DOF) of a kinematic-chain. Why? A dyad has two Parts and three Joints: + Two Parts: 2 × +3×DOF = +6×DOF + Three Joints: 3 × –2×DOF = –6×DOF Thus, total DOF = +6 + (– 6) = 0 (Perfect) Or, use the Gruebler's Equation:
•+ One Motion-Dimension FB controls 1 coordinate. Thus: Mobility = # DOF – # Motion-Dimension FBs = 1 – 1 = 0 (Perfect) Or use the Kutzbach Equation:
Thus the dyad is kinematically-defined and solved. |
||
Top-Tip
If possible, as you build kinematic-chains that you need to control with one Motion-Dimension, do the following steps: 1.Add a Motion-Part 2.Add a dyad #1 3.Change Dyad Closure, if required. 4.Add dyad #2, for a more complex kinematic-chain. 5.Change Dyad Closure of dyad 2, if required. After each step, the mechanism is kinematically-defined and solved. This will help you and MechDesigner. |
Notes:
1.The magic colors are: Green = OK ; Blue = NOT OK. 2.We do not need to know if the Joint is a Pin-Joint or a Slide-Joint. 3.If you joint the two Parts in a dyad to one other Part, you will design a structure. 4.If the kinematic-chain is kinematically-defined before you add a Motion-Part, it will be kinematically defined after you add a Motion-Part, also. 5.If the kinematic-chain is kinematically-defined before you add a dyad, it will be kinematically defined after you add a dyad, also. |