General Approach
Let’s assume:
•You have a spring or element with known linear stiffness, (e.g., in N/m).
•It is connected to a mechanism (like a four-bar linkage, slider-crank, or any jointed system).
•You want to know the effective stiffness at another point in the mechanism.
Understand the Mechanism Geometry
Determine how a displacement at one point causes a displacement at the point of interest (that is, where you want to refer the stiffness).
Let:
• - be the displacement at the location of the actual spring
• - be the displacement at the output or desired location
• - is the transmission ratio or displacement gain
Example
•You have a linear stiffness.
•You attach a lever arm of to the point where the linear deflection is measured.
•A deflection results in a torque ().
•This deflection corresponds to a specific angle.
•The torsional stiffness is then the torque divided by the angle in radians:
.
Transform the Stiffness
Stiffness is defined as:
But you want to express it at a point where the displacement is
The force at the output will transform accordingly:
So the effective stiffness referred to the output point becomes:
Or
•If the displacement is amplified through the mechanism (), the referred stiffness decreases.
•If the displacement is reduced (), the referred stiffness increases.
Suppose you have a torsional spring in a four-bar linkage, and you want to refer its stiffness to a linear output.
1.Compute the angular displacement at the spring (stiffness element)
2.Relate that angular displacement to the linear displacement at the output.
3.Use the chain rule to get the displacement gain .
4.Apply the formula:
Note:
•For rotational stiffness, use angles instead of linear displacements.
•If you have multiple degrees of freedom or nonlinear motion, use Jacobian matrices
where:
• : Original Stiffness matrix
• : Jacobian from the spring location to the point of interest
Referring Stiffness across a Lever
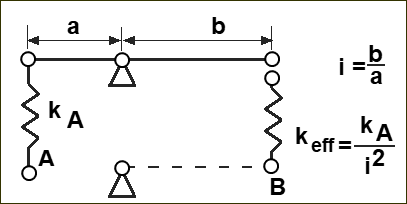 Reduction of Spring's Stiffness 'across' a Lever Ratio Use the Potential-Energy of a Spring to equate the Spring-Rates at points A and B.
|