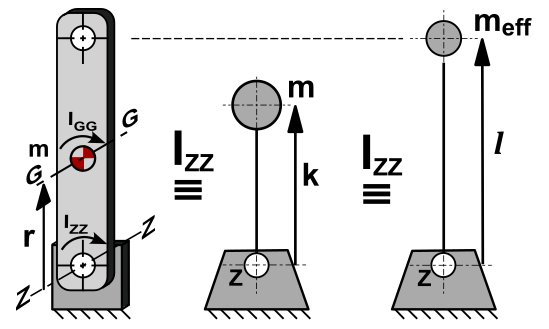
Modeling a Rotating Link
Refer Mass and Stiffness to an Point or Axis
To reduce a multi degree-of-freedom model to a single degree-of-freedom model, we must refer the mass moment-of-inertia and torsional-rigidity, or mass and linear stiffness, of each Part in a kinematic-chain to a single mass and stiffness at the Follower. In this way, you
You must transform the values in such as a way that the dynamic properties of the one degree-of-freedom model are equivalent to the original many degrees-of-freedom model.
Mass Moment-of-Inertia
To calculate the Force to Accelerate a body along a straight-line, you must know the Mass of the body.
To calculate the Torque to Accelerate a body about an axis-of-rotation, you must know the Mass Moment of Inertia of the body about the axis-of-rotation.
Mass Moment-of-Inertia of a point-mass
The Mass Moment-of-Inertia of a Point-Mass (a mass at a point) about an axis-of-rotation is equal to the product of the Mass and the square of its Radius from the axis-of-rotation.
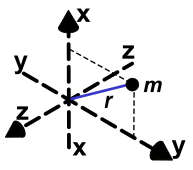 Point Mass at Radius |
Note A Point-Mass is an idealized concept of a finite mass reduced to a single point, without any physical size - is it a Black Hole? |
Mass Moment of Inertia of a distributed mass.
If we consider a solid body as a distribution of elemental masses about a chosen rotational-axis, then the Mass Moment-of-Inertia of the solid body is the sum of the product of each elemental mass and the square of its radius from the rotational-axis.
Mass Moment of Inertia of geometric shapes
Simple geometric shapes have standard formulas that you can use to evaluate the Mass Moment-of-Inertia, usually about at the Center-of-Mass and about the axis perpendicular to the rotational plane.
Example: the Mass Moment-of-Inertia, , of a rectangular, prismatic body, that rotates about an axis, , that is perpendicular to a plane, and through the Center-of-Mass*, is: |
|
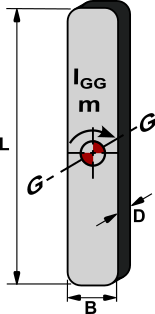 Extruded Rectangle |
The mass is:
* Center-of-Mass = Center-of-Gravity in a constant gravitational field. |
Parallel Axis Theorem, Mass Moment of Inertia about a parallel axis.
We can use the Parallel Axis Theorem to calculate the Mass Moment-of-Inertia about any axis that is parallel to . The image below shows the rectangular link, but now it rotates about the axis , which is parallel to . We use the Parallel Axis Theorem to calculate the Mass Moment of Inertia of the link about the axis . |
|
Parallel Axis Theorem |
|
The Concept of Radius-of Gyration.
It is sometimes useful to redefine the Mass Moment of Inertia as a Point-Mass at a particular radius from the axis of rotation. When the mass of the Point-Mass is equal to the actual Mass of the Solid-Body, we can calculate the radius at which to position the Point-Mass such that its Mass Moment of Inertia is equal to that of the solid body, about the same axis of rotation. |
|
To calculate the Radius-of-Gyration, , we need to know the Mass Moment of Inertia about an axis. In this case we know the value of from:
|
|
Note: If the Mass Moment of Inertia is about a different rotational-axis, e.g. , the Mass Moment of Inertia changes AND the Radius-of-Gyration, , will also change. |
|
The Concept of Equivalent-Mass.
It is sometimes useful to define a Radius for a Point-Mass from an axis of rotation, such that the mass of the Point-Mass is different to that of the solid body, but its Mass Moment of Inertia is equal to that of the solid-body about the same axis of rotation. We assume we know the Radius at which we want to put the Point-Mass from the axis-of-rotation. For example, we want to refer the Mass Moment of Inertia as a mass at the end of a lever, such that Mass Moment of Inertia of the lever does not change. |
|
|
|
|
|
Transforming Masses across a Lever-Ratio to give equal Mass Moment of Inertia
Referring Masses across a Lever
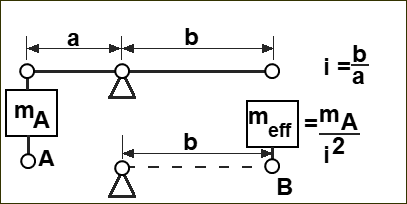 Reduction of a Mass 'across' a lever ratio Use the Kinetic-Energy of a Mass to equate the Mass at points A and B.
|
Referring Springs across a Lever
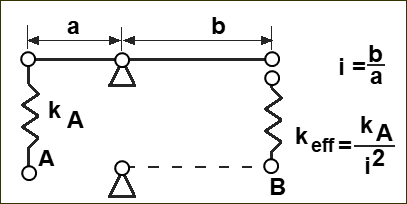 Reduction of a Spring across a Lever Ratio Use the Potential-Energy of a Spring to equate the Spring-Rate at points A and B.
|