General Design Information > Cam-Mechanism Design > Dynamics of Cam Mechanical Systems > Example 6: Power Calculation for Cam Mechanism

Power Calculation

Cam Mechanism - rotating cam, bell-crank, rack-pinion

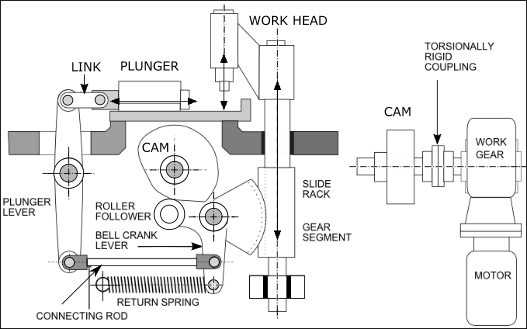
This example machine has a single, force-closed, cam with a swinging roller follower.

The cam operates two mechanisms. The follower is designed as a Bell-Crank. The Bell-Crank drives a:

•Plunger, operating horizontally, with a linkage transmission

•Work-head, operating vertically, with a rack and gear segment transmission

The Plunger moves horizontally against a friction force.

The Work-head and its rack and slide are lifted.

The roller follower is held in contact with the cam by a spring. The spring is strong enough to provide the operating force for both mechanisms.

The motion-law is a Cycloidal motion.

Design Note: The Cam drives the two tools 'positively' away from the 'danger zone' - the Plunger is moved to the left, and the Work-head is moved upwards. The spring pulls the tools into the danger zone. If there is a jam, the Follower cannot 'return' its move with the cam. This is likely to prevent further damage to the mechanisms.

The cam is driven at 60RPM, by a motor and worm gear with a 24:1 ratio. The motor is an AC Squirrel Cage motor running at 1440RPM.

The Challenge:

Find the peak loading in the rise period of the cam - the most heavily loaded period - which occupies 72º of camshaft rotation.

The Lift segment period =

The mechanism does not distort the Cycloidal Motion-Law very much.

The rigidity of the output transmission is estimated to be approximately .

Find also the cam torque and the required size of the electric motor to provide sufficient power and input inertia.

Component or Assembly	Parameter	Value	Units
Bell-Crank lever, roller follower and rocker shaft assembly	Distance form Pivot to Conn-Rod	100	mm
	Distance from Pivot to Follower Center	100	mm
	Inertia about Pivot	0.0231	kg.m2
	Angular Stroke	22.62 (0.395)	º (rad)
	Efficiency	90	%
Connecting Rod	Mass including end joints	0.75	kg
	Linear Stroke	40	mm
Plunger Lever	Pivot to Conn Rod	200	mm
	Pivot to Plunger	160	mm
	Inertia about Pivot	0.0747	kg.m2
	Angular Stroke	11.31 (0.197)	º (rad)
	Efficiency	95	%
Plunger and Link	Mass	3.24	kg
	Slide Friction Force	3.15	N
	Linear Stroke	32	mm
Gear Segment	Pitch Circle Radius	110	mm
	Inertia about Pivot	0.0855	kg.m^2
	Angular Stroke	22.62 (0.395)	º (rad)
	Efficiency	98	%
Work-head, rack and slide Assembly	Mass	18	kg
	Slide Friction Force	41	N
	Linear Stroke	43.5	mm
Return Spring	Spring-post to Pivot	150	mm
	Force at Extended Length	300	N
	Force at short working length (pre-load)	120	N
	Linear Load	60	mm

Output Loading

Convert all loadings to values referred to the bell crank lever, to simulate a simple oscillating mechanism.

The instantaneous velocity of a component is the Motion-Law Velocity factor at that point in the motion multiplied by the 'Stroke of the component ÷ by the motion period (time)'.

Since the period and velocity factor are the same for all components, the velocity of a component is proportional to its stroke, and velocity ratios are the same as the stroke radios.

Equivalent Inertia Calculations

	Conversion	kg.m^2
Bell Crank	no conversion required
Connecting-Rod
Plunger Lever
Plunger Assembly
Gear Segment	no conversion required
Work-head Assembly

Equivalent Torque Calculations

In the Rise Period, for a Cycloidal motion-law is . The output stroke is , and the period is

Therefore, the maximum acceleration of the bell-crank lever in the rise period is:

The inertia torque referred to the bell-crank, is:

Natural Frequency Calculation

The natural frequency of the system can be estimated from the inertia and the rigidity to allow for dynamic response vibration :

Period-Ratio is :

The Torsion-Factor is found with the Torsion Factor Empirical Equation :

Non-inertia and Inertia Load Ratios

Plunger Assembly Friction :
Work-head slide Friction :
Spring-force maximum :
Maximum non-Inertia load:
Spring force minimum :
Minimum non-inertia load (the spring pre-load):
Pre-Load Ratio :
Inertia Ratio :

Peak Output Torque Loading

Load Mix Coefficient
The Peak Output Loading on the bell crank is:

Load Mix Coefficient

The Peak Output Loading on the bell crank is:

Input Loading

Input Torque Coefficient :
The peak input torque (on the cam), allowing 90% cam and follower efficiency, is:
The most economical drive unit is a worm gear with a 4-Pole Squirrel Cage Motor. It runs at 1440RPM at full speed (50Hz Supply). There must be a reduction gear ratio of1440/60 = 24:1 Gear Ratio. The 24:1 worm gear unit has a typical forward efficiency of about 75% and reverse efficiency of 30%.
Peak Power :
The motor with sufficient full-load power to cover this peak power must allow for the reduction gear efficiency of .
A standard motor will be adequate. However, if we assume there is enough inertia at the input shaft, then we can choose a motor that has only the average power. We must consider the efficiency of . The maximum power is reduced.
Reduced Maximum Power :
We can choose a standard motor. We should check the input inertia.
The estimated camshaft, cam, coupling and worm-wheel inertia (all running at 60RPM) is The motor and worm-shaft armature inertia is estimated at .
The equivalent input inertia referred to the cam is:
The minimum inertia required to be sure that the speed fluctuation is not more 10% is found from:
In this case the input inertia at is greater than , and therefore enough to make sure the speed variation is less than 10%. It is interesting to note, however, that without the high speed motor inertia it is probable that the speed fluctuation would be unacceptable. In this example, the calculations are for rotary motion on the bell-crank. To design the Cam and Follower we must estimate the contact force. The peak force on the follower in the direction of motion (that is, the useful force) is the peak torque divided by the length of the bell-crank arm:

This must be divided by the Cosine of the Cam Pressure Angle to get the Contact Force, which can then be checked against load capacity of the Cam.

Input Torque Coefficient :

The peak input torque (on the cam), allowing 90% cam and follower efficiency, is:

The most economical drive unit is a worm gear with a 4-Pole Squirrel Cage Motor. It runs at 1440RPM at full speed (50Hz Supply).

There must be a reduction gear ratio of1440/60 = 24:1 Gear Ratio.

The 24:1 worm gear unit has a typical forward efficiency of about 75% and reverse efficiency of 30%.

Peak Power :

The motor with sufficient full-load power to cover this peak power must allow for the reduction gear efficiency of .

A standard motor will be adequate. However, if we assume there is enough inertia at the input shaft, then we can choose a motor that has only the average power. We must consider the efficiency of . The maximum power is reduced.

Reduced Maximum Power :

We can choose a standard motor.

We should check the input inertia.

The estimated camshaft, cam, coupling and worm-wheel inertia (all running at 60RPM) is

The motor and worm-shaft armature inertia is estimated at .

The equivalent input inertia referred to the cam is:

The minimum inertia required to be sure that the speed fluctuation is not more 10% is found from:

In this case the input inertia at is greater than , and therefore enough to make sure the speed variation is less than 10%. It is interesting to note, however, that without the high speed motor inertia it is probable that the speed fluctuation would be unacceptable.

In this example, the calculations are for rotary motion on the bell-crank. To design the Cam and Follower we must estimate the contact force.

The peak force on the follower in the direction of motion (that is, the useful force) is the peak torque divided by the length of the bell-crank arm:

This must be divided by the Cosine of the Cam Pressure Angle to get the Contact Force, which can then be checked against load capacity of the Cam.