Objectives
To explain •the concept of a dyad, dyad-closure, and how to change the dyad-closure. •how dyads can break! •why that when a kinematic-chain is kinematically-defined before you add a dyad, it is also kinematically-defined after you add a dyad. A dyad is also called an Assur Group in some kinematic journals. |
What is a Dyad:
 5 elements in the R-R-R dyad |
A dyad is: 2 × Parts + 3 × Joints |
In the image, we can see the five elements in a this dyad are: 2 × Parts ( + 3 × Pin-Joints ( This dyad is one of 5 Planar dyads. We model different dyads later in the tutorials. |
Dyad: Degrees-of-Freedom and Mobility.
A dyad does not change the degrees-of-freedom of a kinematic-chain. A Part on a Plane that is free of joints has three degrees-of-freedom(DOF). A dyad has two Parts. Therefore: + 3 DOF × 2 Parts = + 6 DOF. A Joint removes two degrees-of-freedom(DOF) from the Parts you join. A dyad has three Joints. Therefore: – 2 DOF × 3 Joints = – 6 DOF Therefore, a dyad does not change the degrees-of-freedoms. of a kinematic-chain. If a kinematic-chain is kinematically-defined, or solved, before you add a dyad, then it is also solved after you add a dyad. |
R-R-R dyad and the KINEMATICS-TREE
Explore the Kinematics-Tree:
|
||||
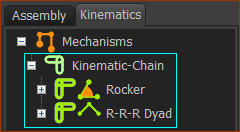 Kinematic-Chain |
Explore the Kinematic-Chain
You can see the Rocker and the R-R-R dyad. Elements in the Rocker - the Motion-Part.
Elements in the R-R-R dyad:
Question: Why R-R-R? Answer: The standard kinematic-term for a Pin-Joint is a Revolute-Joint. Therefore, the letter R in the dyad is for Revolute. Therefore, the R-R-R dyad is identical to a dyad with three Pin-Joints. The R-R-R dyad is one of 5 Planar dyads. We model different dyads later in the tutorials. |
|||
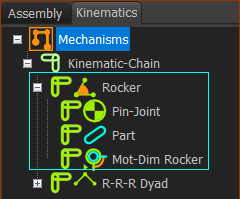 Rocker in the Kinematic-Tree |
||||
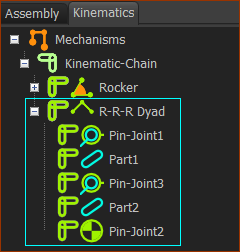 R-R-R dyad in the Kinematic-Tree |
||||
Dyad-Closures
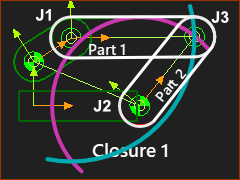
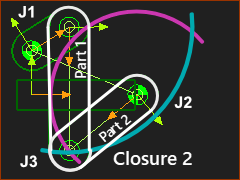
Usually, you can change how you assemble the two Parts in a dyad. Each assembly of a dyad is called a dyad-closure. When you add the last joint in a dyad, we assemble the Parts for you in one of the dyad-closures. If the dyad-closure is not the dyad-closure you want, you must use the Change Dyad-Closure tool. |
|
|
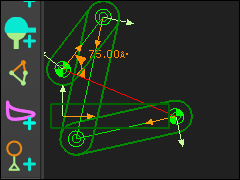
The white Part-Outlines are the two Parts in the dyad: Part 1 and Part 2. J1, J2, and J3 are the three Pin-Joints. Part 1, and J1 •The position of J1 is fixed at the end of the Rocker. •Before you add J3, Part 1 can rotate freely about J1. •J3 must be on the ARC Part 2, and J2 •The position of J2 is fixed in the Base-Part. •Before you add J3, Part 2 can rotate freely about J2. •J3 must be on the ARC When we add J3: J3 can only be where ARC intersects ARC. ARC intersects ARC at two places, Therefore, there are two possible Dyad-Closures for the R-R-R dyad. |
How to Change the Dyad-Closure
When you add the last of the three Joints in a dyad, we assemble for you the Parts in one of the dyad-closures. Use Change Dyad-Closure to assemble the Parts in the dyad-closure that you do want |
|||
 |
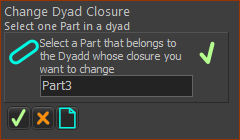
STEP 1: Start the command
The Command-Manager indicate you must select a Part |
||
 |
STEP 2: Select the Part
STEP 3: Complete the Command
|
||
 |
|||
 |
The dyad is now assembled in the different dyad-closure. The R-R-R dyad has two closures. To move the dyad to the original dyad-closure, do STEP 1-3 again. |
||
Dyads that can NOT solve - Dyads an break
When you add the last joint in a dyad, it is possible that the dyad cannot build successfully. |
||
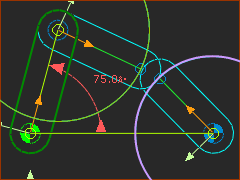 |
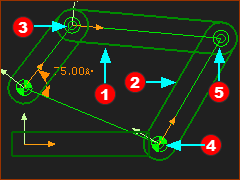
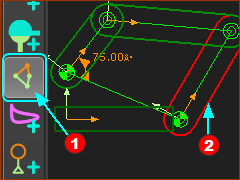
In this image, the R-R-R dyad cannot possibly solve when you add the last Pin-Joint. You can see that the two Arcs (that represent where the end-Points of the Parts) cannot intersect. Note: The two Arcs may intersect at a different period of the machine-cycle. E.g. The Motion-Dimension for the Rocker is 75º. If we decrease the angle to 30º, then the dyad can solve. |
|
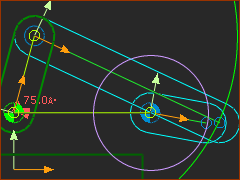 |
In this image, the R-R-R dyad cannot possibly solve when you add the last Pin-Joint. You can see that the two Arcs (that represent where the end-Points of the Parts) cannot intersect. Note: The two Arcs may intersect at a different period of the machine-cycle. E.g. The Motion-Dimension for the Rocker is 75º. If we increase the angle to 100º, then the dyad can solve.
|
|
Dyad Symbols in the Kinematics-Tree
|
||
Kinematics-Tree Symbols
|
Unrestricted Dyad Closure : |
The dyad can solve throughout the machine-cycle. |
|
Restricted Dyad Closure : |
The dyad cannot solve for a period within a machine-cycle, but at a different machine-angle. |
|
Broken dyad : |
The dyad cannot solve now at this machine-angle. |
Extra: Grashof Criterion
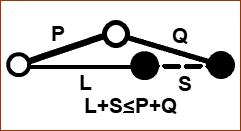 Stretched. |
When the the sum of the shortest and longest bar of a four-bar is less than or equal to the sum of the remaining two bars, then the shortest bar can rotate fully with respect to a neighboring bar. S: length of shortest bar, L: length of the longest bar; P and Q : lengths of the other two bars. Stretched 1.S + L ≤ P + Q Overlapping 2.Q ≤ P + (L – S) 3.P ≤ Q + (L – S) I would recommend you look on-line to study the Grashof Criterion, if this is important to you. In packaging machines, more often than not, the input does not rotate 360. |
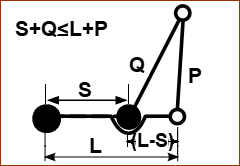 Overlapping |
Video of Tutorial STEP 2.1.A
Rocker + R-R-R dyad - 2 VALID Closures
R-R-R dyad - 2 Valid Closures
Rocker + R-R-R dyad - 2 INVALID Closures (Broken Closures)
R-R-R dyad - 2 Invalid Closures