Hypotrochoid Curves are traced by a Point on a gear that rolls around the inside of a fixed gear.

The shape of the Hypotrochoid Curve depends on the ratio of the gear-teeth. With gears, the ratio is a rational number. Therefore, the curve will repeat eventually, even if the gear ratio is a ratio of two prime numbers.

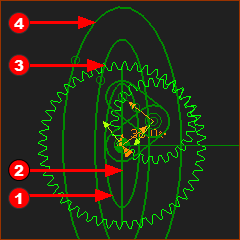
The Orbiting Gear is half the diameter of the fixed gear: 1 : 2

Curve is the Hypocycloid

The Point is on the pitch-circle of the Orbiting Gear - it moves along a straight line.

Hypotrochoid Curves

The Hypotrochoid Curves are ellipses.

Curves are from points on the outside the pitch-circle .

Curve is from a point on inside of the pitch-circle.

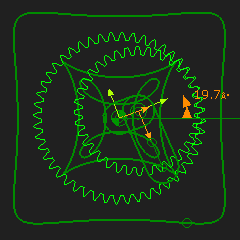
The revolving gear inside has 36T:  the outside gear has 48T

Hypocycloid

The point is on the pitch-circle

Hypotrochoid

The image has two curves of points outside the pitch-circle.

You can see the curve is near to a square.

You can use the Euler-Savary Equation to calculate the best distance from the center of the orbiting gear to give a curve with the best straight-line curve.

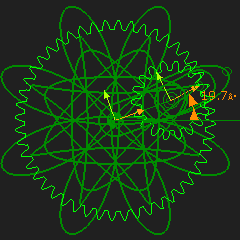
Hypocycloid

One curve that is given by a point on the pitch-circle - it is the Hypocycloid

The Gear Ratio is 48:18