Epitrochoid Curves are traced by a Point on a gear that rolls (orbits) around the outside of a fixed gear.

The curve is called an Epicycloid if the point is on the pitch-circle of the rolling gear.

The curve is called an Epitrochoid if the point is not on the pitch-circle of the rolling gear.

If the point is inside of the Pitch-Circle, it is called Contracted (also Curtate), and if outside the pitch-circle it is called Protracted (also Prolate).

The shape of the curve depends on the ratio of the teeth. With gears, the ratio of the teeth is always a rational number. Therefore, the curve will always repeat, eventually, even if the gear ratio is a ratio of two prime numbers.

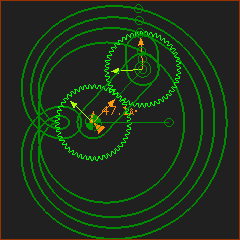
Equal Number of Gear Teeth.

This curve is called a Limaҫon. The image has four curves.

Epicycloid - a point on the pitch-circle of the orbiting gear.

Prolate Epitrochoid - by points outside the pitch-circle.

Curtate Epitrochoid by points inside the pitch-circle.

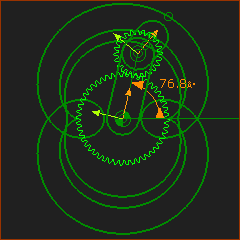
The External Gear is half the diameter of the fixed gear.

The image has four curves.

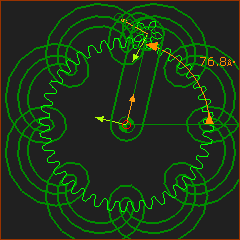
The ratio is 8: 1

There are three curves.

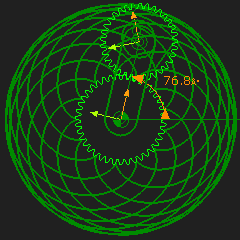
The ratio is 13:12

There is one curve