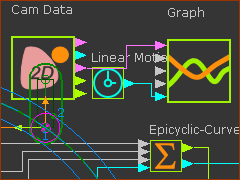
Plot the Radius-of-Curvature for the Cam we have found for the Epitrochoid Curve
A plot of a curve's Radius-of-Curvature is a good example because Radius-of-Curvature needs the Velocity and Acceleration Equations for the X and Y coordinates.
We must symbolically differentiate the Velocity Equations, given in Step 18.2, to find the Acceleration Equations.
Remember, MechDesigner does these calculations automatically with Gear-Pair. We are doing this with a Math FB only as an example of how to use the Math FB.
Plot the Radius-of-Curvature
|
|
Before we can plot the Radius-of-Curvature for a 2D-Cam, we must add a Cam-Data FB
1.Mechanism-Editor : Click , then click the graphics-area
2.Mechanism-Editor : Open the Cam-Data dialog , then click the 2D-Cam. Close the Cam-Data dialog
The 2D-Cam is now linked with the Cam-Data FB
3.Mechanism-Editor : Click , then click the graphics-area.
4.Mechanism-Editor : Drag a wire from the Radius-of-Curvature to the Graph input-connector.
5.Open the graph (see below)
You can see the graph for the Radius-of-Curvature is nonsense.
|
|
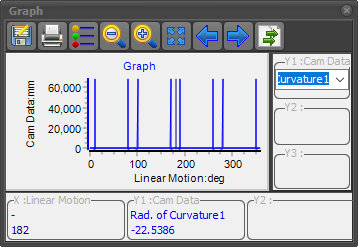 Radius of Curvature - it is not correct |
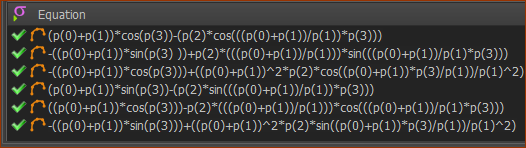
The Parametric-Equations for the X-axis and Y-axis Acceleration Components
Differentiate the X and Y parametric Velocity Equations with respect to Θ.
These are the two Parametric Equations for the X and Y Velocity Components:
PXacc = -(a+b) * cos(Θ) + ((a+b)/b)2 * h * cos(((a+b)/b) * Θ)
PYacc = -(a+b) * sin(Θ) + ((a+b)/b)2 * h * sin(((a+b)/b) * Θ)
As before we must replace:
a with p(0) ; b with p(1) ; h with p(2) ; Θ with p(3)
In the Math FB they are:
Q0[Acc] = -((p(0)+p(1)) * cos(p(3))) + ((p(0)+p(1))^2 * p(2) * cos((p(0)+p(1)) * p(3) / p(1)) / p(1)^2)
Q1[Acc] = -((p(0)+p(1)) * sin(p(3))) + ((p(0)+p(1))^2 * p(2) * sin((p(0)+p(1)) * p(3) / p(1)) / p(1)^2)
Remember, you can cut and paste these equations as the Acceleration Equations in the Math FB.
|
|
Enter the Parametric Equations for the Acceleration Components in the Math FB
|
|
These are the 6 equations for the two output-connectors
•Equations 1, 2, 3: Position, Velocity, and Acceleration Equations for the X -axis
•Equations 4, 5, 6: Position, Velocity, and Acceleration Equations for the Y-axis |
|
Look again at the Plot for Radius-of-Curvature
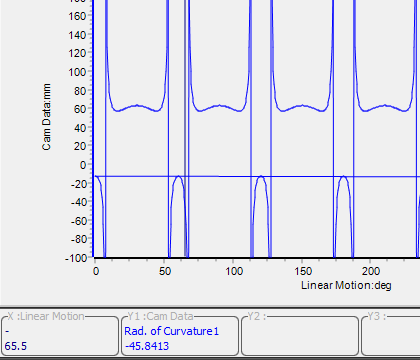 Radius-of-Curvature is now correct. |
We can now see the the plot for the Radius-of-Curvature is correct.
|