Contact Stress...Static-Load Capacity and Low Cycle Fatigue.
This topic does not explain fatigue that leads to pitting. It is limited to the lower end of the Fatigue-Life : 1 < Number of Cycles ≤103.
Tresca Maximum Shear Stress Failure Criterion
As we increase the contact-force/payload between the cam and the Follower-Roller, the weaker material will eventually deform plastically rather than elastically.
To specify the critical load at which the weaker material fails plastically, we need to use a yield.
There are two failure criteria we can use to specify when a metal yields: the Tresca Shear-Stress Failure Criteria and the von-Mises Strain-Energy Criteria.
We will use the Tresca Maximum Shear-Stress Failure Criterion.
Simplified, the Tresca Shear-Stress failure criterion tells us that a metal Yield (fails) due to Shear-Stress when the Shear-Stress is equal to half the Yield-Strength, which results from a normal tension test.
Equation 1 = Yield Strength = Shear Strength Yield-strength has different symbols in different data-sheets, e.g.: |
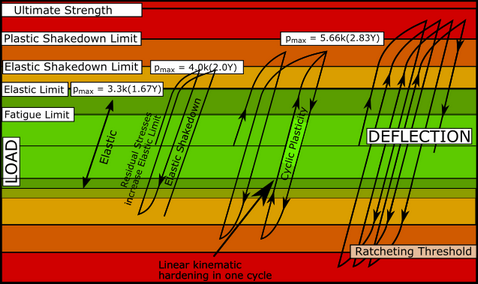
Elastic Limit, or Onset of Plasticity (Contact Stress ≈ 1.6×Y)
|
||||||||||||||||
When a body begins to yield, we say it is at the onset-of-plasticity. We know that:
If you increase contact-force such that the Contact-Stress and the Maximum Shear-Stress is equal to the Shear-Strength, then the Maximum Shear-Stress is equal to half of the Yield-Strength. That is:
LINE-CONTACT There is Line-Contact between a prismatic Cam-Profile and a Cylindrical Follower-Roller.
ELLIPTICAL-CONTACT There is Elliptical-Contact between a Cam-Profile and a Barrel or Crown Follower-Roller. The Stress at which plasticity starts is not very different to Line-Contact. But, it is not as deep as Line-Contact.
|
Elastic Shakedown (1.6×Y < Contact Stress <2×Y)
When
Even if some yield takes place, there will only be a small change to the shape. This is because the yield occurs beneath the surface and the plastic zone is surrounded by a region in which the stress and strains remain elastic. This limits the plastic deformation since the plastic strains must be similar to adjacent elastic strains. The amount of steel that is flattened (moved) by Plastic Strain under the contact must be equal to the expansion of the surrounding steel with Elastic Strain. The first time that the elastic limit is exceeded at a point on the cam, a small plastic deformation occurs. When the Follower-Roller is further along the cam, and the load becomes zero again, residual stresses remain in the cam, below the surface. When the Follower-Roller passes the same point on the cam a second time, the cam stress is the combined action of contact-stress + residual stress from the first pass. Because residual stresses are usually 'protective', the cam is less likely to yield when the Follower-Roller makes a second pass than the cam was when the Follower-Roller made its first pass. (Note: according to theory not presented here: 'if it is possible for residual stresses to occur, they will always occur'). It is possible, that after a few rotations of the cam, the contact becomes elastic, because of the build-up of the protective residual-stresses. This process is called Elastic Shakedown. The new Elastic-Limit after Shakedown can increase to: , compared to for the Elastic-Limit before Elastic-Shakedown. Other factors that help Shakedown: Strain-Hardening: where the cam strains, it may Strain-Harden. Thus, its yield-strength also increases. Note: Strain-Hardening is not Elastic-Shakedown. Steels that already very hard may in fact tend to Strain-Weaken, while those that are soft will tend to Strain Harden Geometric-Changes: if the cam-steel deforms, then the Cam-Profile and Follower-Roller conform with each other. A flat cam becomes cup-shaped when the Follower-Roller is barrel-shaped, for example. The conformity decreases the contact-stress because the Equivalent Radius-of-Curvature, , increases. It turns out that the Hertzian Contact Stress, must be less than or equal to for Elastic Shakedown to occur. This means that if the contact stress is:
...then, Elastic Shakedown will occur. Also, as the load is proportional to , it follows that the ratio of the Shakedown Force limit, , to the Elastic Force Limit, , is given by
This means that the actual load can be increased by ~50% more than the load that is needed to bring about yield on the first machine cycle. |
Full Plasticity (Contact Stress > 2.83×Y)
As the contact stress increases, the plastic zone grows until eventually it reaches the cam surface. Full Plasticity occurs when the Contact Stress reaches the surface. The Contact Stress is then:
|
Shakedown, Ratcheting, Traction / Friction between the Follower-Roller and the Cam-Profile
|
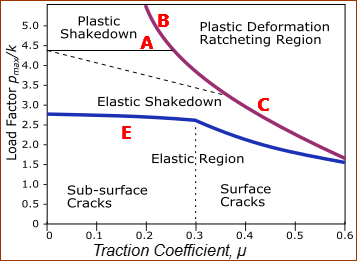
A : Upper Bound to elastic-shakedown limit against alternating plasticity B : Upper Bound to plastic shakedown limit against incremental growth. C : Upper bound to elastic shakedown limit against incremental growth of surface strain E : Elastic limit - Lower bound to elastic limit. |
Traction Coefficient, μ, has an effect on the maximum value and the depth of the maximum shear stress. If the Follower-Roller slides and rolls over the cam, then the friction force moves the maximum shear stress nearer to the surface and also increases its value. When traction or friction is zero, the maximum shear-stress is at 0.78×b (contact half width). At a Coefficient-of-Friction , the maximum shear stress moves to, or very near to, the surface. Thus, plasticity is not constrained by the elastic hinterland. You can see in the image, that the range between the stress when there is 'first yield' (Blue line) and that for 'shakedown' (Magenta line) becomes narrower as you increase the coefficient of friction and there is sliding at the contact. |
|
