Getting Started Tutorials - MechDesigner > Tutorial 13: Forces: Introduction

A Rocker and a Spring

In this topic, you balance the force that acts on the Rocker with a Spring.

You balance the

•Downward Force and Clockwise Moment on the Rocker that result from Gravitational Force

with ...

•an Upward Force and Counter-Clockwise Moment on the Rocker from a Spring FB

A Spring FB exerts a force between Points (called anchor-points) that are in two different Parts. In this case, we need an anchor-Point in the Rocker and an anchor-point in the Base-Part. The Rocker is stationary.

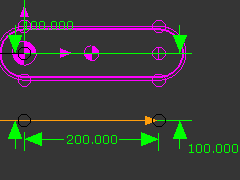
GST-Rocker-Forces-5A

STEP 1: Edit the Base-Part to add a Line

1.Edit the Base-Part

2.Part-Editor: Add a horizontal Line so that its end-Point is 100mm below the end-Point of the Rocker.

3.Close the Part-Editor

TOP-TIP: You can use Tools menu > Show other Kinematic and Sketch-Elements to see the Rocker when you edit other Parts in the Part-Editor.

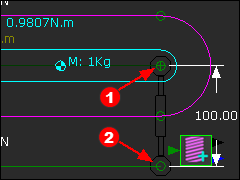
STEP 2: Add a Spring FB

To add the Spring FB you must click a Point in two different Parts

1.Mechanism-Editor: Click the end-Point of the CAD-Line in the Rocker and not the center-Point of the Arc(+)

2.Mechanism-Editor: Click the end-Point of the Line in the Base-Part that is 100mm below the Rocker

The Points become the Anchor-Points for the Spring FB.

GST-Rocker-Forces-6

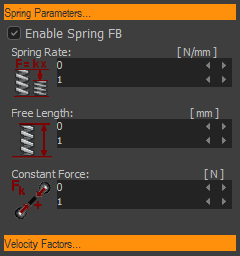
Dialog-FB-SpringForce-SprPara

STEP 3: Enable the Spring FB

1.Mechanism-Editor: Double-click the Spring FB in the graphic-area to open the Spring FB dialog

2.Spring FB dialog: Click to expand the Spring Parameters separator

3.Spring FB dialog: Enable Spring FB check-box

4.Spring FB dialog: Click to close the Spring FB dialog

GST-Rocker-Forces-7

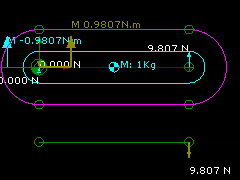
The image to the left shows the Spring FB and the Symbol that represents the Spring.

The Spring FB does not exert a Force, yet. Thus, Force Vectors are not at the Spring's anchor-points.

Constant Force

We can balance the Gravitational Force if we enter a Constant Force in the Spring FB dialog.

A positive Constant-Force pulls the Spring's anchor-points. (o>>>+<<<o)

A negative Contact-Force pushes the Spring's anchor-points (o<<<–>>>o)

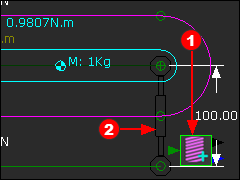
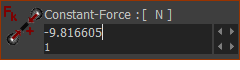
STEP 4: Edit the Spring FB to enter a Constant-Force= –9.80665N

1.Mechanism-Editor: Double-click the Spring FB in the graphic-area to open the Spring FB dialog

2.Spring FB dialog: Click the Spring Parameters separator to see its parameters.

3.Spring FB dialog: Constant-Force enter –9.80665

4.Spring FB dialog: Click to close the Spring FB dialog

–9.80665N exerts a Force upwards against the Rocker.

-9.8066N
Negative Force pusshes Point apart

GST-Rocker-Forces-8

Add the Vertical Forces acting on the Rocker (upwards +ve).

R2(N) - 1(kg)*9.807(m/s/s) + 9.807(N) = 0; R2 = 0N

Add the Horizontal Forces acting on the Rocker (Point 2) : (upwards +ve).

R2H(N) = 0; R2H = 0N

Take Moments about Z-axis at the Rotational Center of the Rocker (Counter-clockwise +ve)

M2 + 0.2(m)*9.81(N) - 0.1(m)*9.81(N) = 0 . Thus M2= -0.981Nm.

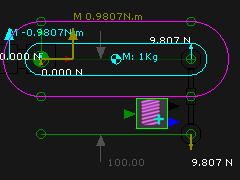
GST-Rocker-Forces-9

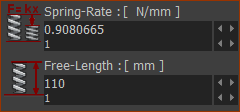
Spring-Rate and Free-Length

You can use the Spring-Rate and Free-Length parameters to give you the same result.

We will enter a Free-Length and Spring-Rate so that the Spring exerts a force equal and opposite to the Gravitational Force.

Also, edit the Constant Force = 0N again.

MD-T13.2.a-SpringRate-FreeLengthipp

When we make the Free-Length = 110mm and the Spring-Rate = 0.980665N/mm, the Spring FB will exert 9.80665N upwards.

Why? The model controls the actual distance between the anchor-points of the Spring FB - the actual distance is 100mm.

Therefore, the model deflects the Spring by 10mm

Therefore, the Spring FB exerts a Force = 10mm * 0.98066N/mm = 9.81N upwards

Note: The Spring FB has:

Two output-connectors :

•Top output-connector = Distance, velocity and acceleration of one anchor-point relative to the other.

•Bottom output-connector =Total Force, X-Force and Y-Force (relative to the coordinate axes of the Mechanism-Plane).

One input Connector :

Optionally, a Force Function at its input-connector from a Math FB.

The Output Data-Type of the Math FB must be set to Force.

Step 13.2: Rocker and a Spring

Step 13.2: Rocker and a Spring

A Rocker and a Spring