Getting Started Tutorials - MechDesigner > Tutorial 13: Forces: Introduction

SLIDER FORCES

This topic uses the Force Vectors: Calculate and Force Vectors : Display tools with a Slider.

•Slider = Part + Slide-Joint + Motion-Dimension FB.

Note:

Motions for this Step: Motions for Tutorial13-1B Download the ZIP file, extract the MTD.

Use MotionDesigner > Open and Append to load the motions into MotionDesigner.

The Slider

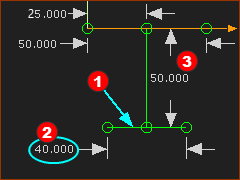Position of a Line in a Part

The top image shows the Slider open in the Part-Editor.

The CAD-Line is 50mm long, at the top. The X-axis (in orange) is over the CAD-Line.

Line is:

40mm long and parallel to the CAD-Line

50mm below the CAD-Line

The bottom image shows the Slider in the Mechanism-Editor

2 collinear Lines in different Parts define the Slide-Joint. One of the Lines is in the Base-Part.

Each Line has a start-Point and end-Point - a total of 4 Points.

The numbers (,,,) identify the 4 Points.

•Line 1 - start-Point and end-Point is in the Base-Part: Its length is 100mm. This Line is horizontal. It supports the Slider.

•Line 2 - start-Point and end-Point is in the Slider: It is 40mm(20+20) long. This Line is 50mm below the CAD-Line.

Mass of the Slider

We add the mass and control the position of the mass with the CAD-Line dialog | Mass Properties tab > User Mass Properties

The Mass of the Slider is 1kg. The Center-of-Mass is 25mm from the start-Point, along the CAD-Line of the Slider.

In this example, the Mass is a Point-Mass - the mass is concentrated at a Point in space (like a Black Hole!). The mass does not have an Inertia or a Radius-of-Gyration.

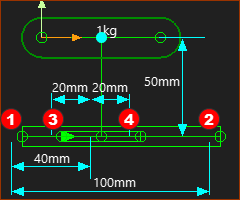4x Point in a Slide-Joint

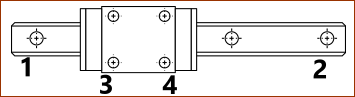Schematic- Linear Slide-Block and Slide-Rail.
Approximate position of Reaction Points

Note:

This is a schematic of a typical Linear Slider Rail with a Slide Block, that you might use in a machine design.

1, 2, 3, and 4 - in the image - are approximately equivalent to the start-Points and end-Points of the two Lines in a Slide-Joint

In your model you should make sure Lines in the Slide-Joint are approximately equal to the length of the Slide-Rail and Slide-Block in your machine.

Calculate and Display Forces

1.Enable Force toolbar > Force Vectors : Calculate - the icon is the same as the icon to the left.

2.Enable Force toolbar > Force Vectors : Display - the icon is the same as the icon to the left.

If a minimum of one Part has Mass, we display for you the Force Vectors. The Force Vectors show the direction, magnitude, and location of each Force.

Note: Click the Force and Torque Vector Scale buttons to increase or decrease the length of the Force Vectors. The buttons are below the graphic-area, in the middle of the Feedback Area.

•There is a Force Vector from the start-Point and end-Point of each Line that you select to add to the Slide-Joint - four(4) Points , and four(4) Force-Vectors.

•The Force-Vectors at a Slide-Joint can ONLY be perpendicular(⊥) to o each Line.

•If the a Slider is a Power Source, then there is a Motive Force-Vector in the direction of the Slider.

CASE 1: Stationary or Constant Velocity Slider

When the Slider moves along the Slide-Joint at Constant-Velocity, the Inertia-Forces are zero. Also, as the Slider is not rotating, the Coriolis-Force and Centrifugal-Force are zero.

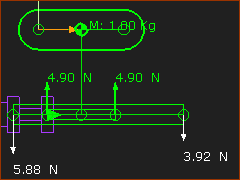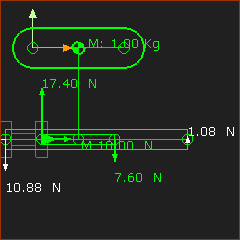
Consider the Forces that act on the Sliding-Part.

•Gravitational-Force: The Slider has a Mass of 1kg. Thus, there is a Gravitational Force = 9.81N. This force vector is not shown.

•Inertia-Force: It is stationary (or moving at a constant-velocity). Thus, the Inertia Force = 0N

The Gravitational Force must be put into equilibrium by reaction forces that act on the Slider.

There are two force-vectors that act upwards that are equal to 4.90N. They ACT ON the Slider. These two Force Vectors are equal because the mass is above the mid-Point of the Slider, and the Slide-Joint is horizontal.

Consider the Forces that act on the Base-Part.

Refer to the dimensions and point numbers in the image at the top of this topic.

The total force acting on the Slider (by the Base-Part) is = 9.81N.

Summation of Moments, about Point :

Summation of Vertical Forces:

These Force Vectors ACT ON the Base-Part, from of the mass of the Slider and its Gravitational Force.

The Force Vectors on the Base-Part as the Slider moves along it with Constant-Velocity.

The forces would be uniformly distributed along the Lines in the two Parts.

However, in MechDesigner, the Forces Vectors are at the start-Points and end-Points at the ends Lines in the Slide-Joint.

CASE 2: Accelerating Slider.

Note: Edit menu > Machine Settings > Cycling Parameters > Cycles/Min to 300.

Link the Motion FB to the ConstAcc motion.

The acceleration of the Slider is 10m/s/s.

GST-13-1B04

Consider the Force Vectors that act on the Sliding-Part.

Gravitational Force, vertical (↑ up+ve ) : .

Inertia Force, horizontal, (—>+ve) :

Summation of Horizontal Forces

These force vectors must be balanced by the reaction force acting on the sliding-part.

Summation of Moments Point

Summation of Vertical Forces ( ↑+ve)

Consider the Force Vectors that act on the Base-Part.

The total force acting upwards by the Base-Part on the Slider is 9.81N.

Summation of Moments at Point

Summation of Vertical Forces

These force vectors ACT ON the Base-Part.