Step 13.3: A Rocker

<< Click to Display Table of Contents >>

Step 13.3: A Rocker

A Rotating Rocker – a Crank

We connect a Linear-Motion FB to rotate the Rocker with a constant angular-velocity.

This Step helps to understand:

•Centripetal Acceleration and Centripetal Force from the circular motion of the Center-of-Mass

•Superposition of Gravitational Force and Centripetal Force

•Why the Moment of the Centripetal-Force equals zero.

Prepare the Model

1.Delete the Spring FB

2.Add a Linear-Motion FB

3.Connect a wire from the output-connector of the Linear-Motion FB to the input-connector of the Motion-Dimension FB.

4.Edit Machine-Settings > Cycling Parameters > Cycles per Minute (RPM) = 60RPM, = 1 Cycle/second = 2π radians/second.

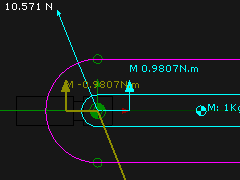
The forces in the mechanism below act at the Pin-Joint - the rotation axis of the Rocker.

GST-Rocker-Forces-10

Summation of Vertical Forces that act on the Rocker

Summation of Horizontal Forces acting on the Rocker (Point 2) : (→ +ve).

Summation of Moments that act on the Rocker:

The Centripetal Force acts on the Rocker through the center of rotation. There it does not exert a Moment on the Rocker.

The Moment that acts on the Rocker is 0.98Nm - see STEP 13.1A

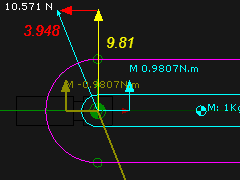
GST-Rocker-Forces-11

When the Rocker is Horizontal

The Horizontal and Vertical Forces are perpendicular(⊥) when the Rocker is horizontal. Hence, we can use Pythagoras:

URL of this topic:
http://mechdesigner.support/index.htm?md-qst13_3-rocker-rotating-rocker.htm