Kinetostatic vs Dynamic Analysis- a definition
A Kinetostatic Analysis1 calculates the forces at joints that are a result of the motions imposed on a mechanism with mass and inertia by an idealized power source2.
A Dynamic Analysis calculates the motions of a mechanism from a force or torque that is imposed on the mechanism with masses and inertia.
MechDesigner does the Kinetostatic Analysis of each kinematic-chain.
MechDesigner 17+ also does dynamic analysis.
Notes
1.Force: is a generalized force, which will include moments.
2.An Idealized Power Source moves the mechanism exactly as planned. A simple example of an Idealized Power Source would be a cam-shaft that rotates at an exact constant-velocity even though the torque on the cam-shaft changes as it rotates.
About Kinetostatic Forces
Kinetostatic-Forces: •Forces at joints •Forces at anchor points of Springs •Forces at the contact point between gear teeth flanks, and between a cam-profile and follower-profile •Force or Torque to move each kinematic-chain with a predefined motion Kinetostatic-Forces are a function of: •The Motion of Parts: Inertia force, Centripetal force, Coriolis force. We assume the motions of all Parts move exactly as planned •The Mass distribution: Mass, Center-of-Mass, Inertia •External Forces: Spring, Drag, Coulomb Forces, ... •Gravitational Force – when the Mechanism-Plane is not horizontal •Which joint has the Power-Source that drives the kinematic-chain. See: Why Configure the Power Source Kinetostatic-Forces do not include: •Impact Forces of Parts that collide •Impact Forces after traversal of backlash in Joints, Gear-Pairs or Cam-Tracks •Friction Forces •Magnetic, Electrical Forces |
Kinetostatic-Forces are for Ideal Kinematic-Chains.
IDEAL KINEMATIC-CHAINS: •Rigid Parts do not bend, twist or stretch •Rigid Parts do not expand with temperature •Rigid-Part have an exact length, without a tolerance •Joints do not have play (backlash) •Joints do not have Friction •Power Source is idealized - it moves exactly as planned •Surfaces at Cams and Gears do not deflect |
REAL KINEMATIC-CHAINS: •Real Parts: do deflect, twist and stretch •Rigid Parts: do expand with temperature •Rigid Parts: do have a tolerance to their length, plus other geometric constraints (GD&T) that need to be applied •Real Joints: do have backlash, play •Real Joints: do have friction •Power Sources do not move exactly as planned •Real contact surfaces do deflect •Real kinematic-chains: are not 100% efficient •Real kinematic-chains vibrate |
You may think “Why do a model when it can deviate from the Ideal Kinematic-Chain by so much”? However, the better your design, the nearer it will be to the Ideal Kinematic-Chain. |
|
Configure the Power Source.
It is important that you Configure the Power Source correctly for each kinematic-chain before you do a Kinetostatic Force Analysis. You must select at which joint (or cam, spring, gear) is the Power-Source of each kinematic-chain. Note: The Moment Vector we show at a joint is the Application Load or Load Torque that the output-shaft of a Servomotor and Gearbox must drive. When you add a Servomotor and Gearbox, you must also accelerate their inertia, and overcome their friction in addition to the Load Torque. In MechDesigner, each kinematic-chain has three different possible Power Sources.
|
To illustrate this, we can use a simple four-bar kinematic-chain. The four-bar includes a: Motion-Part. •A Rocker. It is the vertical Part on the left. •The Rocker has a 1kg mass that is 50mm horizontally to the left of the Pin-Joint made with the Base-Part. Its weight is ~9.81N (1kg * 9.81m/s/s = 9.81N). R-R-R dyad (two Parts, three Pin-Joints) •one Part is horizontal, the other Part is vertical and parallel to the Rocker. |
|
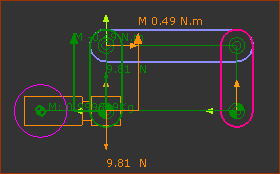 Configure Power Source to the Left |
Configure Power Source 1: LEFT Pin-Joint with the Base-Part. Resolve Forces: 9.81N Vertical Down Gravitational Force Down 9.81N Vertical Up Reaction Force at Pin-Joint The Forces at all of the other Joints are ZERO. Resolve Moments: 0.49Nm Counter Clockwise Torque from the weight of the Mass at 50mm from Pin-Joint. 0.49Nm Clockwise Torque from the Motor that acts-on the Rocker to balance the Weight |
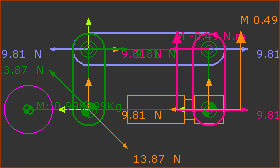 Configure Power Source to the Right |
Configure Power Source 2: Right Pin-Joint with the Base-Part Resolve Forces: Vertically and horizontally to give forces at the Pin-Joints. The force due to the mass is transmitted through the kinematic-chain to the Power-Source. Resolve Moments: Resolve Moments gives the same Moment (Torque), but at the Pin-Joint on the right. You can see that the Forces for 1 are different to 2.
|