Step 13.1A: Stationary Rocker

<< Click to Display Table of Contents >>

Navigation:  Getting Started Tutorials - MechDesigner > Tutorial 13: Forces: Introduction  >

Step 13.1A: Stationary Rocker

Forces that ACT ON a Rocker.

To understand how we calculate for you and show the Forces Vectors, we will start with a basic kinematic-chain.

•The kinematic-chain is a Rocker

•The Base-Value of the Motion-Dimension FB controls the angle of the Rocker.

•The Motion-Dimension FB does not have a wire connected to its input-connector.

•We add a Profile / Extrusion to the Rocker, The Extrusion has mass and inertia.

Add the Model

A Rocker with Center-of-Mass Symbol(1) with Forces Display ON

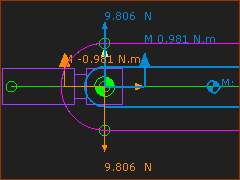
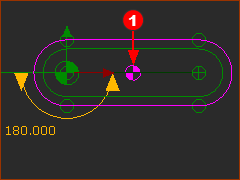A Rocker with Center-of-Mass Symbol(1) with Forces Display ON

STEP 1: Add a Rocker

1.Mechanism-Editor: Edit the Base-Part

2.Part-Editor: Geometry toolbar > Add a Line, Add Dimension | Drag to add the Line, dimensions to locate the line and define its length.

3.Part-Editor : Constraints toolbar > Add Horizontal to make the Line horizontal. Close the Part-Editor

4.Mechanism-Editor : Kinematic elements toolbar > Add Part | Drag to add the Part

5.Mechanism-Editor : Kinematics-elements toolbar > Add Pin-Joint | Click the start-Point of the Part, and the end-Point (the right-side Point of the horizontal Line) in the Base-Part.

6.Mechanism-Editor : Kinematic FB toolbar > Add Motion-Dimension FB | Click the Pin-Joint, the Lines in the Base-Part and the Part, OK-tiny-11-15 the Command-Manager.

STEP 2: Add a sketch-loop, and a Profile/Extrusion.

1.Edit the Rocker Part

2.Part-Editor : Geometry toolbar > Add Lines / Add Arcs (40mm Radius) | to add a sketch-loop. Do the Hover+Drag technique to merge the end-Points of each sketch-element (see Tutorial 3)

3.Part-Editor: Geometry toolbar > Add Coincident Constraints | to move the center-Point of each Arc to the start-Point and end-Point of the CAD-Line along the Rocker

4.Part-Editor: Geometry-Editor | Edit the length of the CAD-Line to equal 200mm. Exit the Part-Editor.

5.Mechanism-Editor: Solids menu (or toolbar) > Add Profile | Click the sketch-loop, Click OK-tiny-13-17 in the Command-Manager.

6.Mechanism-Editor : SHIFT-CLICK the Profile

7.Selection-Window: In the Selection-Window, Right-click the Extrusion element, Click Edit element to open the Extrusion dialog.

8.Extrusion dialog >  Mass-Properties : Edit the Density = 4756kg/m3 with the Extrusion Depth =10mm to make the Mass of the Extrusion = 1kg*

9.Close the Extrusion dialog.

* From the shape of the Extrusion, we calculate for you its Mass(kg), its Moment-of-Inertia(kg.m2), and its center-of-mass.

In this case, because the sketch-loop is symmetrical and equal to the length of the Part - the center-of-mass is 100mm from the Start-Point of the CAD-Line in the Part.

The symbol for the center-of-mass is the GST-PointSymbol - see image above Red-14-1b

Calculate and Display the Force Vectors

There are two icons in the Force toolbar: Calculate and Display Force Vectors.

GST-Icon-Force-Calculate-ON

Mechanism-Editor: Click Force toolbar > Calculate Forces

GST-Icon-Force-Vectors-Show

Mechanism-Editor: Click Force toolbar > Display Force Vectors

When a minimum of one Part has mass, we calculate for you, and display Force Vectors.

The Force-Vectors give the direction, location, and magnitude of each Force.

Notes

Use the Force and Torque Vector Scale buttons to increase or decrease the length of the Force Vectors. .

Analyze the Forces

GST-13-1A01

Force Analysis - Information:

•Action / Reaction Force-Vectors at each joint.

•Moment at the Pin-Joint, which is equivalent to the Load-Torque or Application-Torque that an idealized Power Source must provide to the Rocker.

•Motor symbol (in Purple) at the Pin-Joint. The Motor symbol identifies the location of the Power Source.

•The Part-Outline and the Force-Vectors that act on a Part are the same color.

•There are two Parts in the model - the Base-Part and the Rocker - therefore, there are two vector colors.

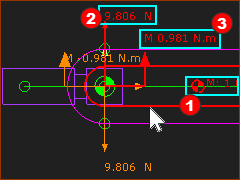
GST-13-1A02

Move your mouse-pointer to the Part-Outline of the Rocker.

You will see that the Force-Vectors that ACT ON the Rocker are Red

Vertical Forces (N) acting on the Rocker - Upwards is +ve

Moments (N.m) at the Pin-Joint - Counter-clockwise is +ve

Force explanation of the RED Force Vectors and Moments

Red-14-1b Gravitational Vector - not shown = 1kg*9.807kg/m/s/s = 9.81N

Red-14-2 Vertical Force - 9.81N acts upwards. The reaction force from the Base-Part that acts on the Rocker. The Rocker would fall freely if the Base-Part did not react to support the Rocker with the vertical Force.

Red-14-3 Counter-Clockwise Moment of 0.98Nm. The Rocker would rotate freely clockwise if the Base-Part did not resist the Rocker with this Torque.

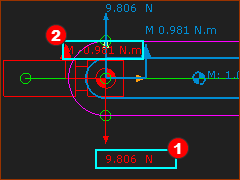
GST-13-1A03

 

Now move your mouse-pointer to the vertical Force-Vector that acts on the Base-Part.

All vectors that ACT ON the Base-Part turn Red.

There is:

Red-14-1b Vertical Force 9.81N downwards, that acts on the Base-Part. This is the Gravitational Force that acts-on the Base-Part.

Red-14-2 Clockwise Moment (Torque) of 0.98Nm that acts on the Base-Part.

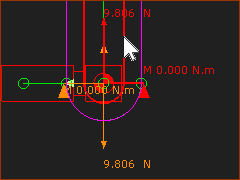
GST-13-1A04

Edit the Motion-Dimension FB to rotate the Rocker until it is vertical

•My mouse-pointer is above the Part-Outline of the Rocker - the Part-Outline and the Force-Vector become Red.

• Vertical Force = 9.807N.

This is the same vertical force as when the Rocker was horizontal. This is not a surprise. The Part has the same mass and it is the only joint through which the force can act.

•Torque Moment = 0Nm

The Center-of-Mass of the Rocker above the Pin-Joint. Therefore, the Rocker does not need a Torque to hold it in the vertical position.