Getting Started Tutorials - MechDesigner > Tutorial 18: Math FB > Step 18.1: Position: Plot an Epitrochoid Curve

Plot the Epitrochoid Curve: Position equations

The Epitrochoid-Curve is a good example. You can compare the Epitrochoid Curve you get from the parametric equations that you enter in the the Math FB to the Epitrochoid Curve you can get from a Gear-Pair.

•The Epitrochoid-Curve given by a Gear-Pair is correct - it is found by MechDesigner!

•The Epitrochoid-Curve from the Math FB is correct - only when the equations are correct.

See Tutorial 14 : Epitrochoid Curve given by a Gear-Pair.

Parameters and Parametric Equations

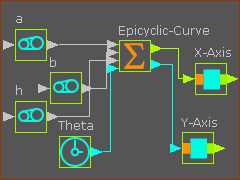
We will add parametric equations to a Math FB to calculate separately the X and Y coordinates of the Epitrochoid-Curve.

One equation will calculate the X–axis coordinates. A different equation will calculate the Y–axis coordinates.

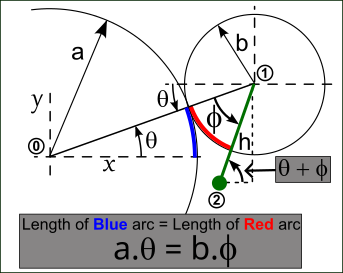
GST-18-101-C

The parametric equations for the family of Epitrochoid curves are:

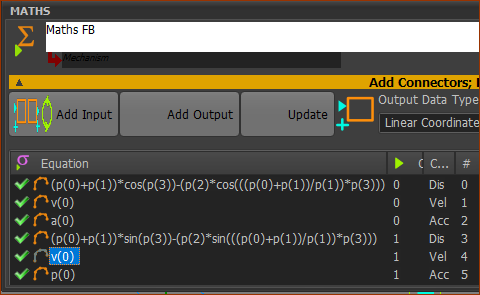
Px = (a+b)*cos(Θ) – h*cos((a+b)/b)*Θ)

Py = (a+b)*sin(Θ) - h*sin((a+b)/b)*Θ)

Parametric-Constants

a = radius of the fixed circle

b = radius of the rolling circle

h = distance to the point 2, from the center of the rolling circle

Independent-Variable

Θ = the independent variable: 0 to 360 (0 or 2×Π)

The parametric equations, above, give the family of Epitrochoid Curves. Thus, if you change a Parametric-Constant - a, b, or h - you will plot a different Epitrochoid-Curve.

To enter parametric-constants in the Math FB, use one of these methods:

Method 1

Enter the actual values for the Parametric-Constant - a, b, h - explicitly in the Math FB dialog.

To plot a different Epitrochoid Curve, you must open the Math FB dialog to edit the parameters again.

Method 2

Add three Gearing FBs and connect wires to the inputs of the Math FB. Edit the Add after Gearing Ratio parameter. The output from the Gearing FB may need to be divided by 1000.

To plot a different Epitrochoid Curve, edit a Gearing FB to edit its parametric-constant.

Method 3

Add the parameters in the Gearing FB to a Design-Set.

Piggyback Sliders and Parametric Equations.

It is convenient to use Piggyback Sliders - one Slider for each set of Parametric Equations

1.Edit the Base-Part and add a horizontal Line; Exit the Part-Editor.

Add Slider-X to move parallel with the X-axis:

2.Add Part; Add Slide-Joint between the Part and the Line in the Base-Part; Add Motion-Dimension FB to the sliding-Part to give Slider-X.

Add a vertical Line to Slider-X:

3.Edit Slider-X; Add a vertical Line that is parallel to the Y-axis; Exit the Part-Editor.

Add Slider-Y to move parallel with the Y-axis of the Base-Part:

4.Add a Part; Add Slide-Joint between the Part and the vertical Line in the Slider-X; Add Motion-Dimension FB to the sliding-Part to give Slider-Y.

5.Rename the two Motion-Dimension FBs to X-axis and Y-axis.

The Piggyback Sliders are now in the graphics-area.

Add a Math FB and Open the Math FB dialog

GST-18-102

Add a Math FB

1.Click Modeling FB toolbar > Add Math FB

2.Click the graphics-area

The Math FB is now in the graphics-area.

Open the Math FB dialog

1.Double-click the Math FB

1.See How to open a dialog

The Math FB dialog is now open.

How many Input-Connectors and Output-Connectors?

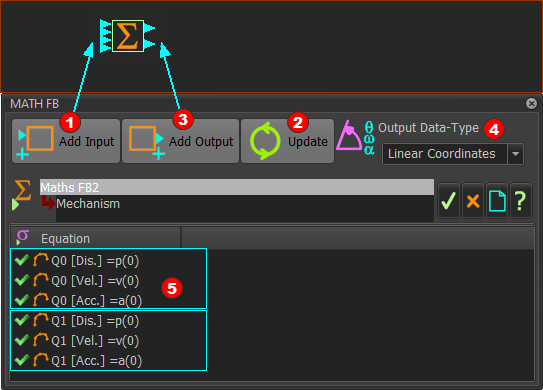
GST-18-103

GST-18-104

Input-Connectors

There are three(3) Parametric-Constants (a, b, h) , and the Independent Variable ()

STEP 1: Add four(4) input-connectors:

1.Click the Add Input button four(4) times.

2.Click the Update button.

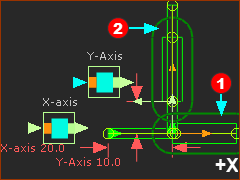
Output-Connectors

We need two(2) output-connectors to output the motions for the X-axis Slider and the Y-axis Slider.

STEP 2: Add one(1) output-connector to give a total of two(2) output-connectors:

1.Click the Add Output button one time, to give a total of two output-connectors.

2.Click the Update button.

Output Data Type

Use Output Data Type to change the units at the output to Linear Coordinates.

STEP 3: Change the Output Data Type to Linear Coordinates:

1.Click the Output Data Type drop-down arrow.

2.Select Linear Coordinates (scroll above Rotary Coordinates).

3.Click the Update button

Default Equations, Data-Channels, Input-Connectors and Output-Connectors

Input-Connectors

Numbers

The input-connector numbers start at Zero (0) for the top input-connector.

The input-connectors numbers, from the top, are therefore : 0, 1, 2, ... .

Data-Channels

All wires that connect Function-Blocks that control motion-values have three Data-Channels.

The Data-Channels labels in the equations for the Input-Connectors

•Parameter label of input Data-Channel 1 is “p” for Displacement, m

•Parameter label of input Data-Channel 2 is “v” for Velocity, m/s

•Parameter label of input Data-Channel 3 is “a” for Acceleration, m/s/s

We combine the Input-Connector Number (0,1,2, ...) and the Data-Channel parameter label (p,v,a) as:

p(0), v(0), a(0) - are the three Data-Channels of the top input-connector

p(1), v(1), a(1) - are the three Data-Channels of the next input-connector

Output Equations

Each equation evaluates one Data-Channel for one Output-Connector.

Because each Output-Connector has three Data-Channels, there are three equations that evaluate the top output-connector.

Numbers

The output-connector numbers also start at Zero (0) for the top input-connector.

In the equations, we prepend the output-connector number with the label “Q”.

In the equations, the Output-Connector Numbers, from the top, are therefore : Q0, Q1, Q2, ... .

Data-Channels

All wires that connect Function-Blocks that control motion-values have three Data-Channels.

The Data-Channels labels in the equations for the Output-Connectors

•Parameter label of output Data-Channel 1 is Dis. for Displacement, m

•Parameter label of output Data-Channel 2 is Vel. for Velocity, m/s

•Parameter label of output Data-Channel 3 is Acc. for Acceleration, m/s/s

We combine the Output-Connector Number (Q0, Q1, Q2, ...) and the Data-Channel parameter label (Dis,Vel,Acc) as:

Q0(Dis.), Q0(Vel.), Q0(Acc.) - the three Data-Channels of the top output-connector

Q1(Dis.), Q1(Vel.), Q1(Acc.) - the three Data-Channels of the one down from the top output-connector

POSITION : Parametric Equations in the Math FB

STEP 1: Enter the Parametric Equations for the two output-connectors

The parametric equations for the family of Epitrochoid Curves are:

Px = (a+b)*cos(Θ) - h*cos((a+b)/b)*Θ)

Py = (a+b)*sin(Θ) - h*sin((a+b)/b)*Θ)

We must re-write these equation with the correct syntax for the Math FB.

Each of the wires we connect to an input-connector has a wire-number (0, 1, 2, 3) and a data-channel (p, v a).

We use the p data-channel for the parameters. The v data-channel of a constant is equal to zero(0). Therefore, in the parametric equations we:

Replace: a with p(0) ; b with p(1) ; h with p(2) ; Θ with p(3)

1.Equation #0 is now ...

Q0[Dis] = (p(0)+p(1))*cos(p(3))-(p(2)*cos(((p(0)+p(1))/p(1))*p(3)))

2.Click the Update button

3.Equation #3 is now ...

Q1[Dis] = (p(0)+p(1))*sin(p(3))-(p(2)*sin(((p(0)+p(1))/p(1))*p(3)))

4.Click the Update button

You can Copy and Paste these equation directly into the Math FB.

To Paste, you must select each equation, right-click it, and select Paste in the shortcut menu.

The equations in the Math FB are now:

GST-T18-1-EpiCurve-3

Function-Blocks for the Parametric-Constant and the Independent Variable

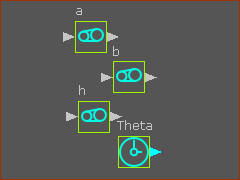
GST-T18-1-EpiCurve-5

Define the 3 Parametric-Constants

1.Mechanism-Editor: Click Kinematic FB toolbar > Add Gearing FBs - do 3 x

2.Mechanism-Editor: Rename each Gearing FB to a, b, and h - see image to the left.

3.Mechanism-Editor: Edit each Gearing FB 'a'

4.Gearing FB dialog: Enter a value for the Add after Gearing Ratio parameter,

5.Close the Gearing-FB

Do 3-5 again and again to enter values also for the Parametric-Constant b, and h.

Note: I have entered a = 120, b = 40, h = 40

<<< Gearing FB dialog : Add after Gearing Ratio for the Parametric-Constant 'a'

Add the Independent-Variable

1.Mechanism-Editor: Click Kinematic FB toolbar >Add Linear Motion FB

The output from a Linear Motion FB increases from 0 to 360.

It will represent the angle, Θ, the Independent-Variable,

See schematic image at the top of this topic.

Connect the FBs

1.Mechanism-Editor: Drag wires from the output of Gearing FB to the respective input-connectors of the Math FB.

2.Mechanism-Editor: Drag a wire from the output of the Linear-Motion FB to the bottom input-connector of the Math FB.

3.Mechanism-Editor: Drag a wire from the Math FB for the X-axis to the input-connector of the Motion-Dimension FB for the Slider that will move parallel with he X-axis.

4.Mechanism-Editor: Drag a wire from the Math FB for the Y-axis to the input-connector of the Motion-Dimension FB for the Slider that will move parallel with the Y-axis.

Add a Trace-Point

1.Mechanism-Editor: Click Kinematic elements toolbar > Trace-Point

2.Mechanism-Editor: Click a Point on Slider-Y of the Piggyback Slider

3.Mechanism-Editor: Click in the Command-Manager.

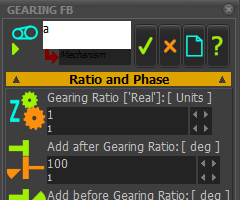Gearing FB: Add after Gearing Ratio parameter

GST-T18-1-EpiCurve-6

Add a Design-Set - select the 3 Parametric-Constants

GST-T18-1-EpiCurve-8

Add a Design-Set and add to it the three Parametric-Constants.

1.Mechanism-Editor: Click Function-Blocks menu > Design-Set, and click the graphics-area.

2.Mechanism-Editor: Open the Design-Set dialog

3.Design-Set: Unlock, and add three Element Rows

4.Design-Set: Click one Element-Row ; Click a Gearing FB - for Parametric-Constant a

Select Property for Design-Set interface opens - see image to the left. In the interface:

5.Select Property for Design-Set : Select OutputStartUnits: Add after Gearing Ratio

6.Select Property for Design-Set: Click to close the Select Property for Design-Set interface.

Do 4 -6 again, and again, to add Parametric-Constants b and h

Video - to show the Epicycloid-Curve family

If we enter 120 for Parameter a, we can enter 60, 40, 30, 20, 10 as factors for Parameter b.

Each will give a continuous, endless, Epitrochoid-Curve.

•If Parameter h = b, there is a cusp in the Epitrochoid-Curve.

•If Parameter h > b, there is a loop in the Epitrochoid-Curve