Getting Started Tutorials - MechDesigner > Tutorial 14: Gear-Pairs / Rack-Pinions > Other Gear Configurations

Geared Five-Bar Mechanisms

Geared Five-bar mechanisms are usually built with:

•One Gear-Pair

•One dyad

Applications

Geared five-bar mechanisms are interesting... to some people. They can give:

•Complex Coupler Curves

•Complex Function Generators

Geared Five-bar Mechanism Configurations

There are four ways you can edit a Geared Five-bar Mechanisms:

1.Gear-Pair: use fixed or orbiting gear centers

2.Dyad: use one of the five dyads: R-R-R, R-R-P, R-P-R, R-P-P, or P-R-P.

3.Gear Mesh: use an external or internal gear-mesh

4.Basic Design: edit the number of teeth on each gear

Typical Geared Five-bar Mechanism Configurations

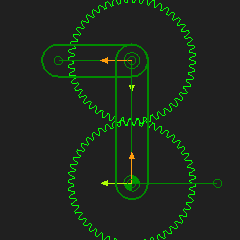
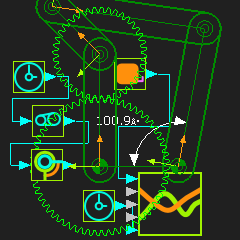
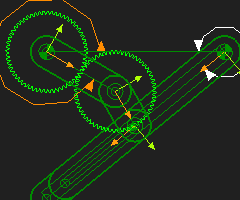
Complex Coupler Curves (Fixed Gear-Pair and R-R-R Dyad)

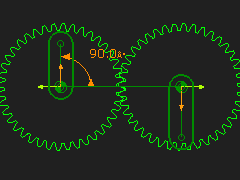
GST-14-Cartwright1

Gear-Pair: 1:1, Fixed-centers, External Mesh

Dyad: R-R-R dyad

Application: Coupler Curve

A Gear-Pair has 3 Parts:

•Base-Part, Input Crank, and Geared-Rocker

A Dyad has two Parts. Typically, the dyad is an R-R-R dyad.

STEP 1: Add a Simple Gear-Pair - Option 1

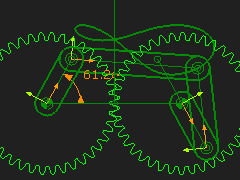
GST-Geared5Bar-1

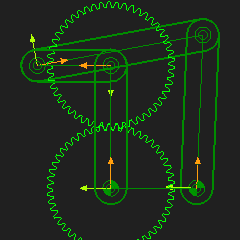
STEP 2: Add an R-R-R dyad

To remind you:

2.a. Add two Parts

2.b. Add three Joints

STEP 3: Edit the Part used for Gear 2

Add a Line that radiates from the center of the Geared-Rocker - the Driven-Gear.

Add dimensions for the length and angle of the Line.

Use the end-Point of the Line for one of the Pin-Joints in the R-R-R dyad.

You can edit the angle of the Line to edit the phase of the Geared Rocker relative to Driving-Gear.

The design parameter options are:

1.Gear Ratio between Gear 1 and 2 (Number-of-Teeth);

2.Phase between the Gears;

3.Length of Driving-Gear and Driven-Gear Parts.

4.Length of each Part in the dyad.

GST-Geared5Bar-2

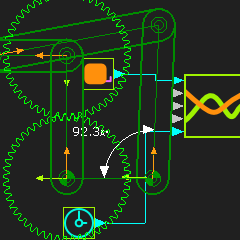
STEP 4: Change the number-of-teeth with the Gear-Pair dialog - for example 60:40.

In this case, it takes two rotations of the input crank to complete the function at the output shaft

To plot the complete Trace-Point, you must rotate the input crank two times faster.

STEP 5: Add a Gearing FB; Gearing-Ratio = 2

STEP 6: Connect the wires between the Linear-Motion FB, Gearing FB and Motion-Dimension FB

STEP 7: Connect the Output from the Motion-Dimension FB to the X input of the Graph FB

GST-Geared5Bar-3

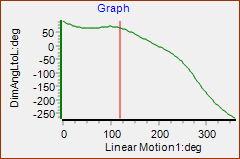
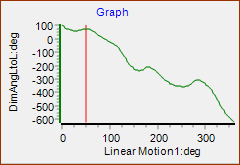
Here is an 'interesting' Coupler Curve.

In these Coupler Curves we are plotting the motion of the middle joint of the R-R-R dyad.

You can add a Point to one of the Parts to give even more complex Coupler Curves.

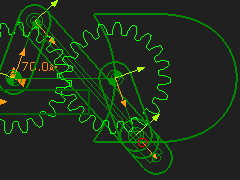
Complex Function Generators (Orbiting Gear-Pair and R-R-R Dyad)

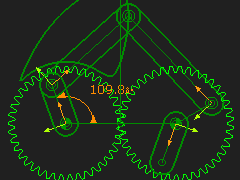
	Gear-Pair: 1:1, Orbiting-centers, External Mesh Dyad: R-R-R dyad Application: Function-Generation Typically, you can get interesting motions from a Geared Five-bar that has a Gear-Pair with an Orbiting center. It is called a Function-Generator. STEP 1: Add an Epicyclic Gear-Pair STEP 2: Make the gear ratio 1:1 (for example 50:50 Gear Teeth)
	STEP 3: Add an R-R-R dyad between the end the Geared Rocker and the Line in the Base-Part
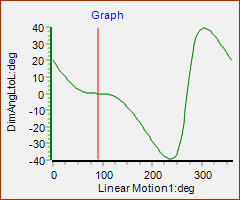
	STEP 4: Measure the angular position of the output Part over a Machine Cycle with a Measurement FB STEP 5: Add a Graph FB STEP 6: Connect the Measurement FB to an input of the Graph FB Add a Design-Set to give a quick way to edit the Part lengths. This Graph is of the Output Shaft Rotation as a Function of the Input, Constant Speed, Shaft Rotation. Notes about Mechanism Synthesis It is typical that an output vs input relationship is given. Then a mechanism is found to provide the function. Four-bar mechanism Function-Generators are limited. For example, it is not easy to synthesize a mechanism that oscillates the output shaft more than one time in a machine cycle. It is clear from this graph that more complex functions are possible.

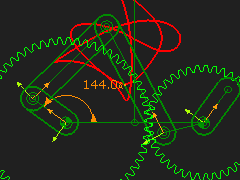
	Change the Gear Ratio to give more interesting Function Generation You can change the gear ratio of the Gear-Pair to give more complex function generation. STEP 7: Change the Gear ratio - for example 60:40. In this case, it takes two rotations of the input crank to complete the function at the output shaft STEP 8: Add a Gearing FB; make the Gear ratio 2 STEP 9: Connect the wire between the Linear-Motion FB, Gearing FB and the Motion-Dimension FB STEP 10: Connect the Output from the Motion-Dimension FB to the X input of the Graph FB
	The Y-axis in the Graph is for two rotations of the crank to give the complete Function-Generation for the 60:40 gearing ratio.

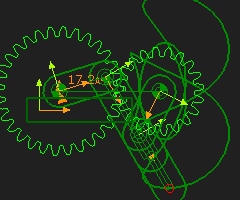
Geared Five-Bars: (Gear-Pair and R-P-R Dyad)

	Gear-Pair: 1:1, Fixed-centers, Internal Mesh Dyad: R-P-R Dyad Application: Coupler Curve
	Gear-Pair, 2:1 Fixed-centers with an R-P-R dyad Application: Coupler Curve •The Gear-Pair ratio changed to 60:40 •The Crank must rotate tow times to complete the Trace-Path •To plot the complete Coupler Curve you should add a Gearing FB before the Motion-Dimension FB and make the Gearing Ratio = 2.
	Gear-Pair 1:1, Fixed-centers, R-R-P dyad. Application: Coupler Curve
	Gear-Pair 1: 1, Orbiting-center, R-P-R dyad Application: Function-Generation
	The motion of the output Rocker as a function of the input-rocker. It has a reasonable dwell.