4-Tooth Sprocket and Polygonal Action

The image shows a schematic of a chain wrapped around a sprocket with 4 teeth.

Radius:

In the top image, the chain is tangent with the Pitch-Circle of the Sprocket - at a radius of

As the sprocket rotates, the component of horizontal velocity reduces.

The minimum  the chain gets to the center of the sprocket is .

Therefore, as the chain moves up and down, the effective radius of the sprocket changes to give an uneven, non-constant chain velocity.

Linear Speed (horizontal)

The linear speed of the chain between the sprockets is a maximum in the top image:

The linear speed of the chain is a minimum in the bottom image:

With 4 teeth, the minimum to maximum velocity changes by approximately 30% !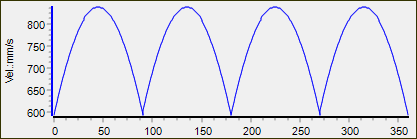

Chain's Linear Velocity as a 4-Tooth Sprocket rotates by 360 degrees

Linear Velocity Discontinuity

You can see in the plot of "Chain's Linear Velocity as a 4-Tooth Sprocket rotates by 360 ", above, that the slope of the chain's velocity changes instantly as each chain-link engages with a sprocket-tooth. The step in velocity is a step in acceleration.

This is an acceleration-discontinuity.

As each new chain-link engages with a sprocket tooth, the linear-acceleration of the chain jumps - it is discontinuous.

When a chain has Polygonal-Action,

•Tension variation in the Chain

As a chain link engages with a tooth, the chain suffers a step change in acceleration. Thus, there is a tension variation.

•The pitch of the chain link is not constant.

Usually, it is recommended that you use more than 17 teeth on a standard sprocket. Bicycle sprockets have fewer, rarely less than 11 teeth. Also, the derailleur compensates for the tension-variation.

Toolbar :

Geometry toolbar > Transition-Curve

Menu :

Geometry menu > Transition-Curve

To add a Transition-Curve

You can see that the Transition Curve is easy to add. However, it is used with Pulleys or Chains.

A Tutorial will show you how to apply the Transition Curve to a Long-Link Chain.