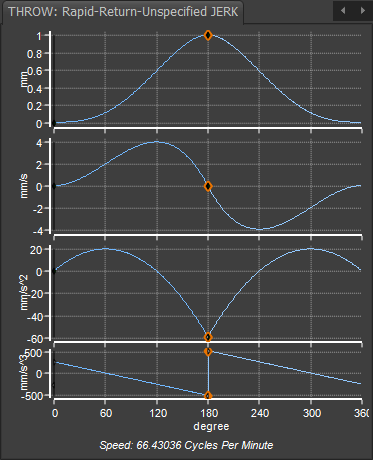
The Throw Motion-Law

Unlike other motion-laws, the Throw motion-law rises from its Start-Position to its maximum displacement, and then returns to its Start-Position.

To give you maximum flexibility, use two Flexible Polynomial segments to design the Throw motion-law. Usually, the two segments have equal durations, but it is not necessary.

Throw: Rapid-Return 1 - Zero Jerk at Start and End.

Because you use two Flexible-Polynomial segments to design the Throw motion-law, you can enter different motion-values and motion-constraints at its start, its maximum displacement, and at its end.

This Throw has a Quick-Return because it has a LARGE negative acceleration, and unspecified Jerk, at its maximum displacement - the transition from Rise to Return.

See also:

•Quick Return 1: Finite Jerk @ Start/End/Mid-Point

•Quick Return 2: Zero Jerk @ Start/End/Mid-Point

•Rapid Return 2: Smooth-Start/End

Two Segment 'Rapid-Return Motion 1

Motion-Values of each motion-derivative

Start of Rise segment 1 :

•Position = 0

•Velocity = 0

•Acceleration = 0

•Jerk = Unspecified ( Actual value = 260.6m/s/s/s )

Middle Blend-Point*:

•Position = 1

•Velocity = 0

•Acceleration = Unspecified (  Actual value = -58.84mm/s/s )

•Jerk = Unspecified ( Actual value = ±521.167mm/s/s/s )

End of Return segment 2 :

•Position 2 = 0

•Velocity = 0

•Acceleration = 0

•Jerk = Unspecified ( Actual value = -260.6mm/s/s/s )

* Edit the X-axis value of the middle Blend-Point to give an asymmetrical motion.