Dialog: Function-Block: Polynomial-Fit

<< Click to Display Table of Contents >>

Navigation:  MechDesigner Reference & User Interface > Dialogs >

Dialog: Function-Block: Polynomial-Fit

Polynomial-Fit FB

See also: Add Polynomial Fit FB

Before you use this tool, I recommend you save your work.

Then save it again with a new model file-name.

About Polynomial FB

MD-Toolbar-Modelling-FB-PolyFit

The Polynomial Fit FB finds a concatenated series of Polynomials (5th order) that are approximately equal to the data at its input-connector.

After you do a Polynomial-Fit, you can:

•Transfer Polynomials directly to MotionDesigner as a new Motion name-tab.

•Connect a wire from the output-connector of the Polynomial-Fit FB to the input-connector of a different FB.

•Export the motion-values that you calculate as a text-file.

•Export the values for position, velocity, and acceleration at the beginning and end of each polynomial segment as a CSV file.

•Export the polynomials segments in a format suitable for the Schneider-Electric EPAS4 servo-controller.

How to open the Polynomial-Fit dialog

MD-GA-PolynomialFitFB

After you add a Polynomial-Fit FB to the graphics-area:

1.Double-click the Polynomial-Fit FB in the graphics-area

OR

1.See How to Open a dialog

The Polynomial-Fit dialog is now open.

Polynomial-Fit dialog

Polynomial-Fit FB dialog/interface.

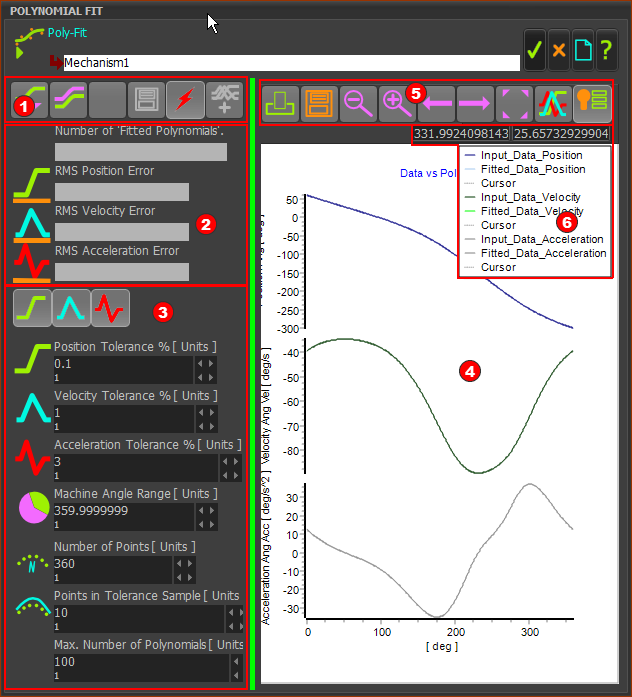Polynomial-Fit FB dialog/interface.

The Polynomial-Fit dialog:

Red-14-1 Acquire and Save Toolbar - acquire and save results.

Red-14-2 Analysis of Results - RMS errors and the number of Polynomials.

Red-14-3 Settings for Polynomial Fitting Algorithms - tolerances, limits, and range for polynomial fitting.

Red-14-4 Graph Plots: for the input-data and the calculated data from the Polynomials.

Red-14-5 Graph toolbar - view and save the graph-data in different ways.

Red-14-6 Graph Legend. - graph plot color scheme for original data and fitted Polynomials, for each motion-derivative

1rAcquire and Save toolbar

Acquire and Save Results toolbar

Acquire and Save Results toolbar

The toolbar buttons are:

Red-14-1 Acquire (Capture, Get One Cycle) :

Click this button to acquire data at the input-connector for one machine-cycle - this is the Raw-Data.

Red-14-2 Fit Polynomials to Data :

Click to Fit Polynomials to the Raw-Data - see Settings for Polynomial Fitting Algorithms.

Red-14-3 Stop Algorithms : (see also Auto-Run)

The algorithms usually fit polynomials within a few seconds. If you do not see the results after a few seconds, then click this button to stop the algorithms.

Red-14-4 Save Coefficients :

Click to save the results to a CSV file, or a EPAS4 file that is suitable for a Schneider Electric servo-controller.

Red-14-5 Auto-Run :

Immediately allow the algorithms to find the polynomials that fit the data to the accuracy as specified, and with less or equal to the maximum number of polynomials.

Red-14-6 Send Polynomials to MotionDesigner :

Send the Polynomials to MotionDesigner as a new motion. Add a new Motion name-tab.

Note on Blend-Point Control-Buttons: After you send the Polynomials to MotionDesigner, none of the Match Control Buttons are active. Instead, the Start motion-value of a segment, is equal to the End motion-value of the previous-segment. Obviously, you can choose to Match the motion-values as part of your motion-design process.

2r2rAnalysis of Results

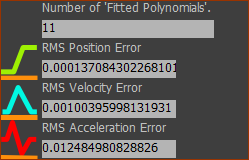MD-Dialog-FB-PolynomialFit-RMSErrors

Number of Fitted Polynomials in Fit (read-only)

The actual number of Polynomials in the numerical solution.

See also: Maximum Polynomial Count in the Settings for Polynomial Fitting Algorithms.

RMS Position Error, RMS Velocity Error, RMS Acceleration Error (read-only).

They give the RMS (Root of the Mean of the Square) error as a percentage for each motion-derivative between the Polynomial that we fit to the data, and the raw-data at the input-connector.

3rSettings for Polynomial Fitting Algorithms

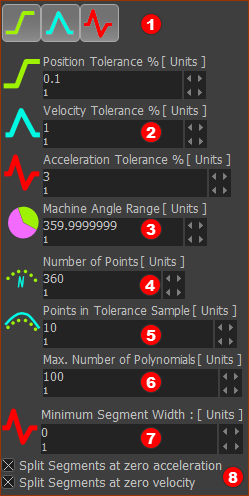MD-Dialog-FB-PolynomialFit-PreFitSetting

Parameters to enter before you click Fit Polynomials to Data (button Red-14-2 in the Acquire and Save toolbar, above)

Red-14-1 Position, Velocity, Acceleration buttons.

Click each button to identify the motion-derivatives to which you want to Fit Polynomials.

Red-14-2 Position, Velocity, Acceleration Tolerance %

Enter the tolerance, as a %, for each motion-derivative, within which the Fitted Polynomials should represent the data at the input-connector.

Red-14-3 Machine Angle Range

Optionally, reduce the range for which you want to calculate Polynomials

Red-14-4 Number of Points

The number of data points that are calculated from the Polynomials, to plot the graphs.

Red-14-5 Point in Tolerance Sample of Points

The number of points that the algorithm uses to fit each polynomial to the data at the input-connector.

Red-14-6 Maximum number of Polynomials.

Upper limit of the number of Fitted-Polynomials in the data.

Red-14-7 Minimum Segment Width.

Lower Limit for the width of a Segment

Red-14-8 Split Segment at Zero Acceleration / Velocity check-boxes

Force the solutions to split the motion (add a new Segment) at which the Acceleration / Velocity crosses zero - positive to negative and vice versa.

5rGraph toolbar

MD-Dialog-FB-PolynomialFit-Toolbar2-ViewandSaveResults

The toolbar buttons are:

Red-14-1 Print Graphs : Print the graphs immediately to the default printer

Red-14-2 Save Graph Data: Save the Data to a text file.

Red-14-3 Zoom Out and Zoom In to the Graph Details

Red-14-4 Pan Left and Pan Right : Click to save the results to a CSV file, or a EPAS4 file that is suitable for a Schneider-Electric servo-controller.

Red-14-5 Zoom Extents

Red-14-6 Toggle display: Plot three separate graphs OR Plot three stacked on-top of each other

Red-14-7 Toggle display: Do show Graph Legend OR Do NOT show Graph Legend

6rGraph Legend

MD-Dialog-PolynomialFit-GraphLegend

Graph plot color scheme for

•original, or input, data

•fitted data calculated from the fitted polynomials

•each motion-derivative

•Cursor - you can click ON a graph of each motion-derivative to show a cursor.

The X-Y data-values of the active cursor is above the graphs.